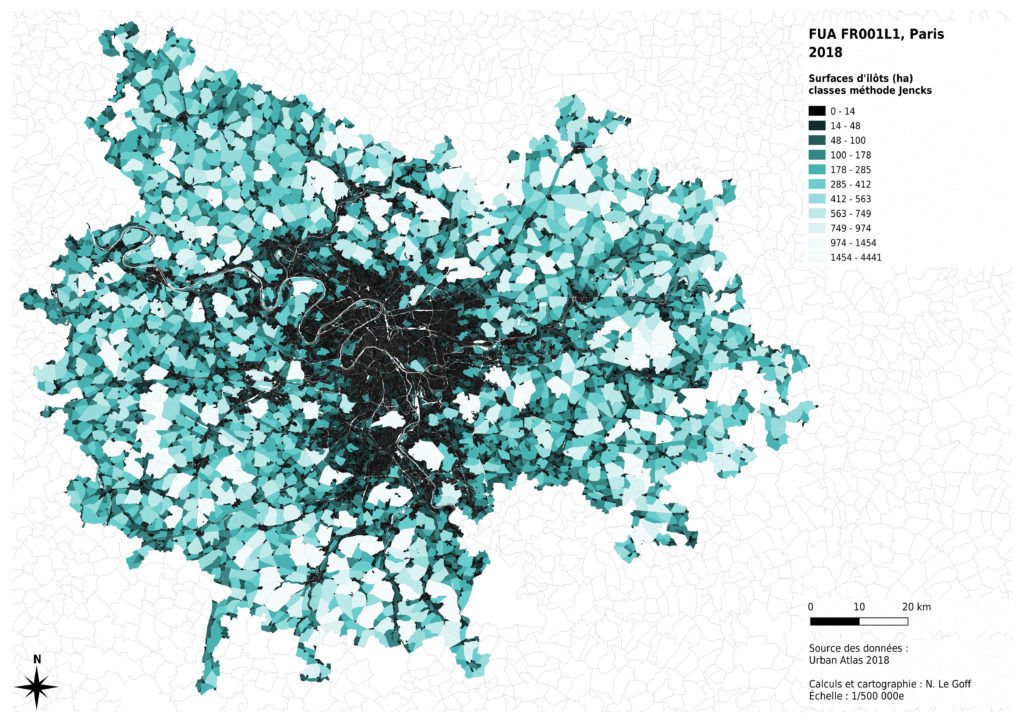
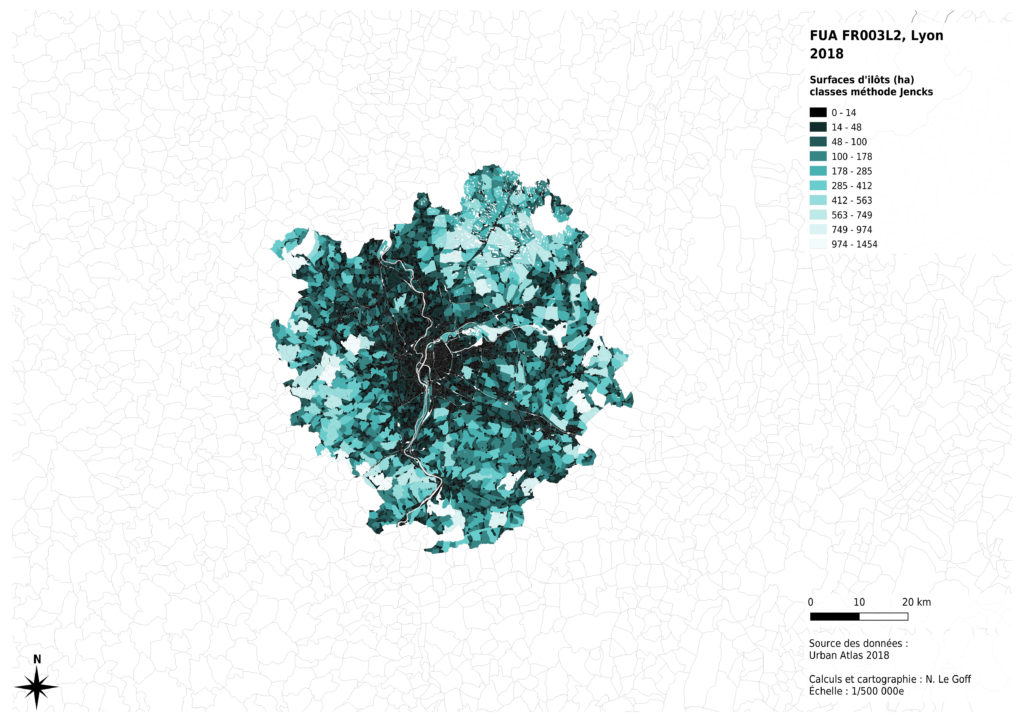
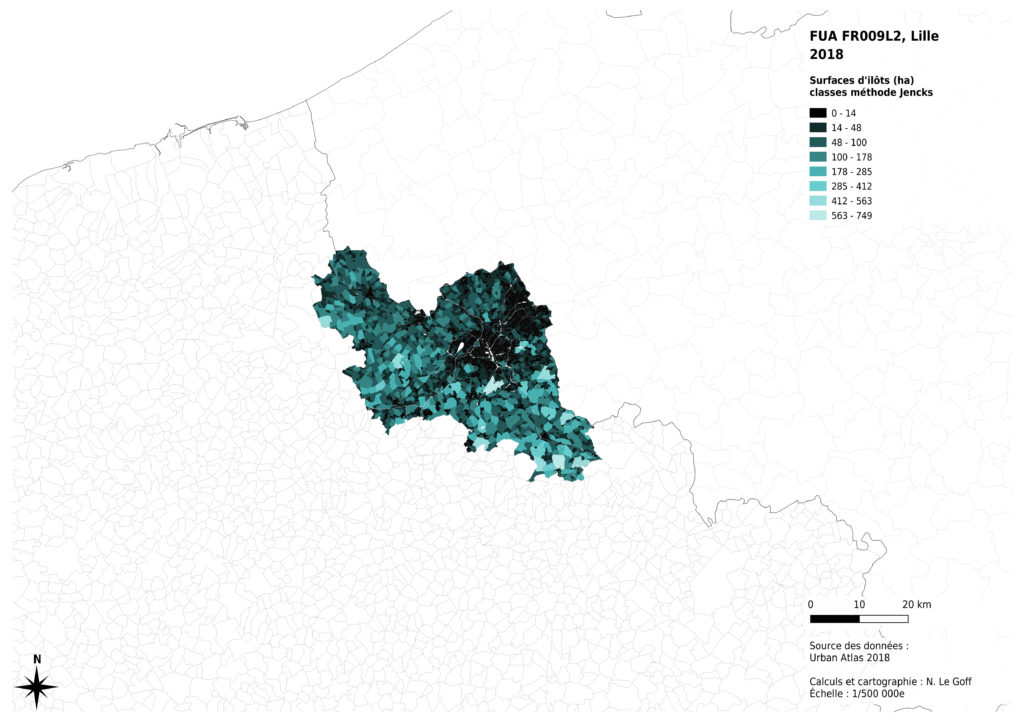
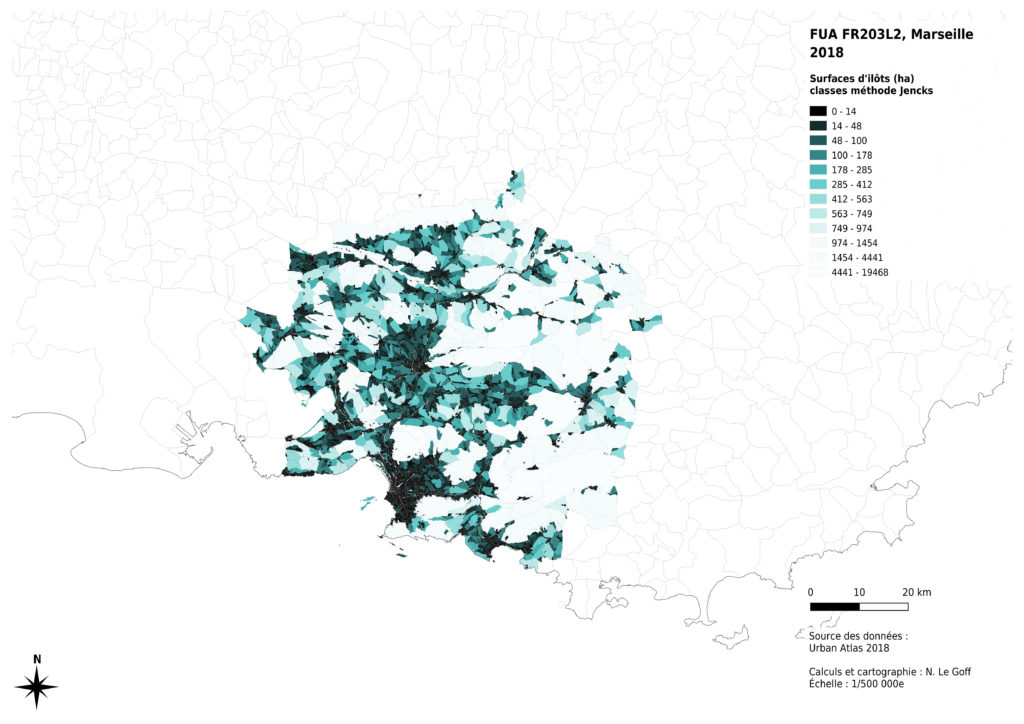
Lorsque les données d’une suite sont très dispersées, il est d’usage d’utiliser, au choix, soit un découpage de classes selon une progression géométrique, soit un découpage selon la méthode de Jencks, soit un découpage selon les quantiles. Les logiciels de Sig proposent, en général ces différentes méthodes, ce qui permet de tester visuellement le résultat obtenus.
Mais comme le souligne, l’article pédagogique de Phillpe Lahousse et Vincent Piédanna, dans sa conclusion, l’application de méthodes statistiques sans esprit critique n’est pas nécessairement le plus pertinent :
« Le document final soit en fait résulter d’une subtile adéquation entre le respect des caractéristiques intrinsèques à sa distribution (en particulier les paramètres de forme), la maîtrise des outils statistiques de discrétisation, la connaissance géographique du phénomène analysé et les objectifs fixés quand à l’information à transmettre. Face à la diversité des situations, aucune solutionne s’impose automatiquement. »
Nous avons donc testé les trois méthodes citées ci-dessus pour déterminer laquelle serait la plus pertinente pour discrétiser les îlots des métropoles étudiées. Et nous avons d’abord conservé le même dégradé pour les différents essais, afin de rendre compte visuellement des différences obtenues.
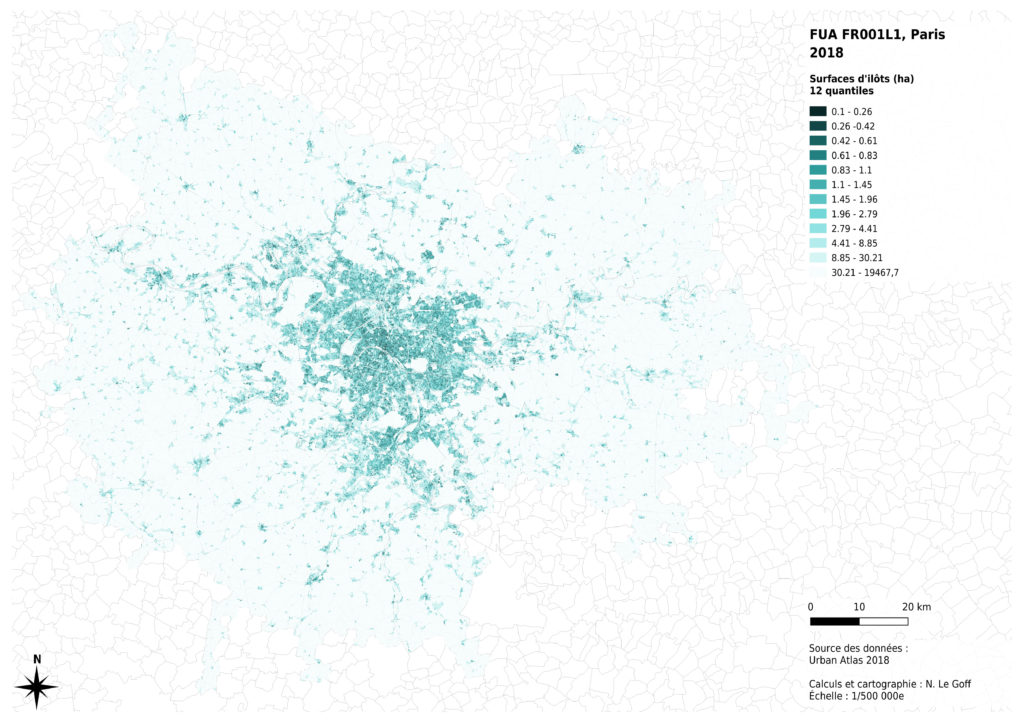
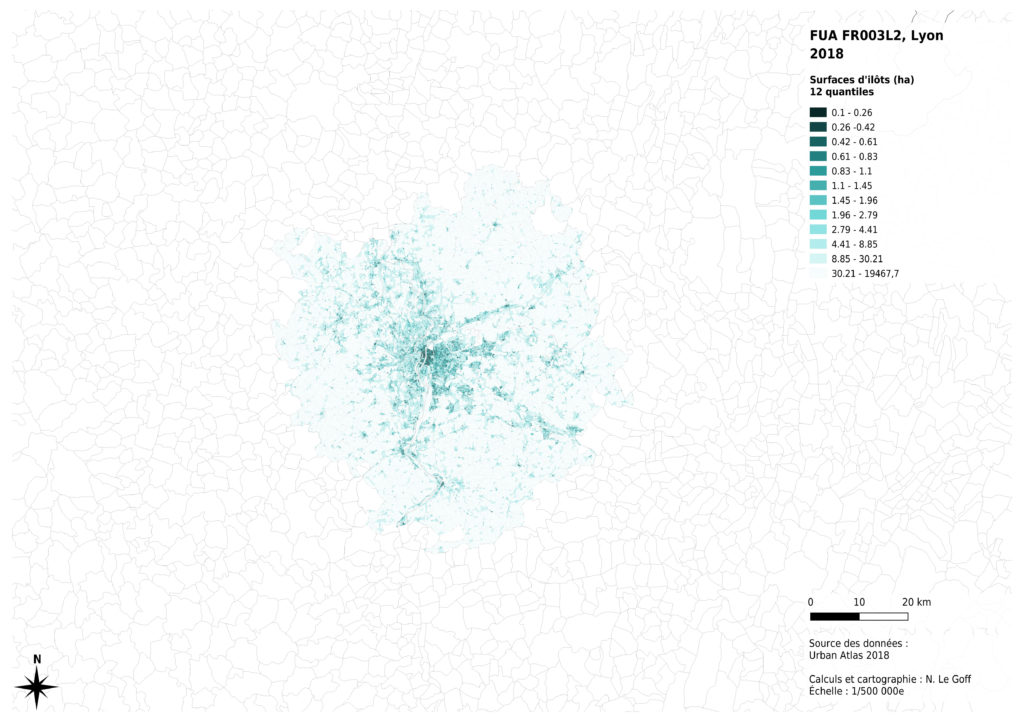
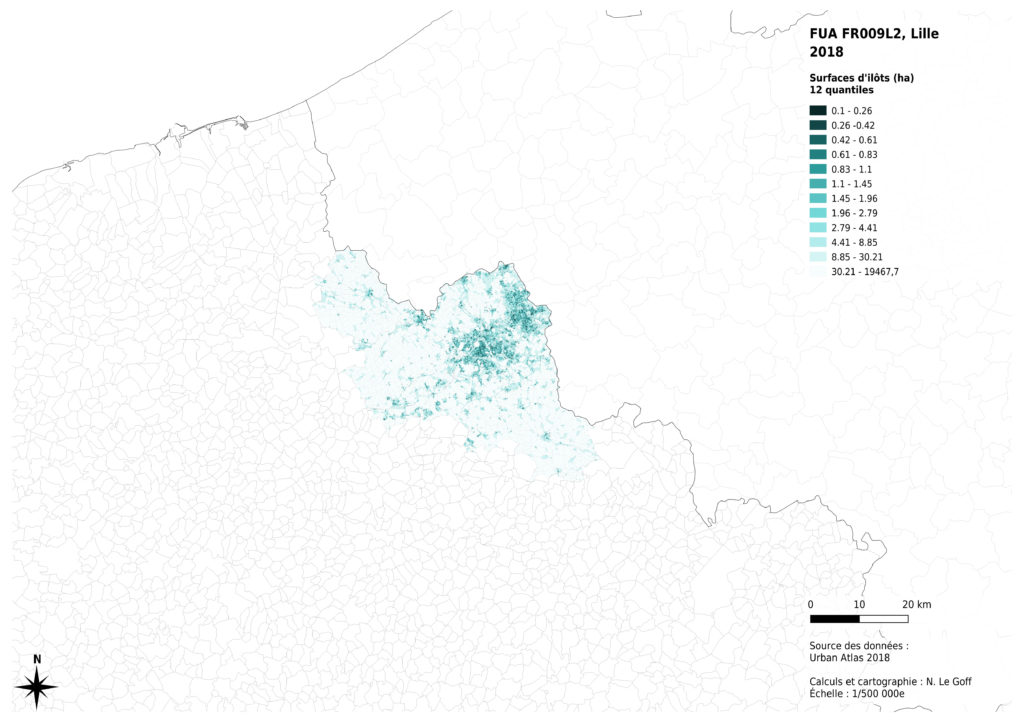
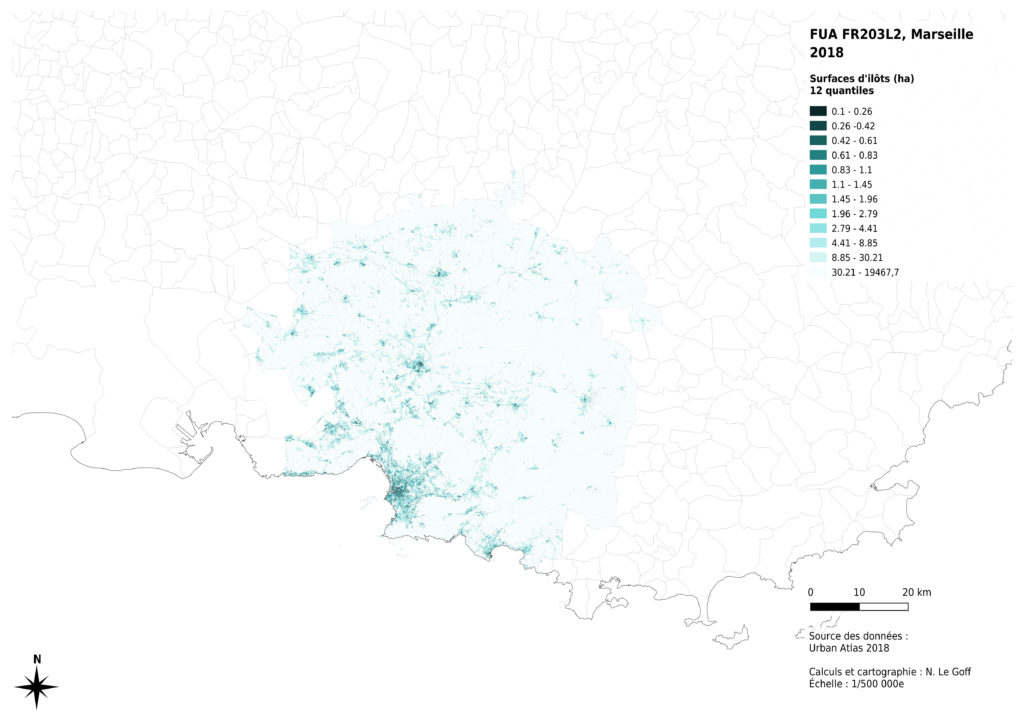
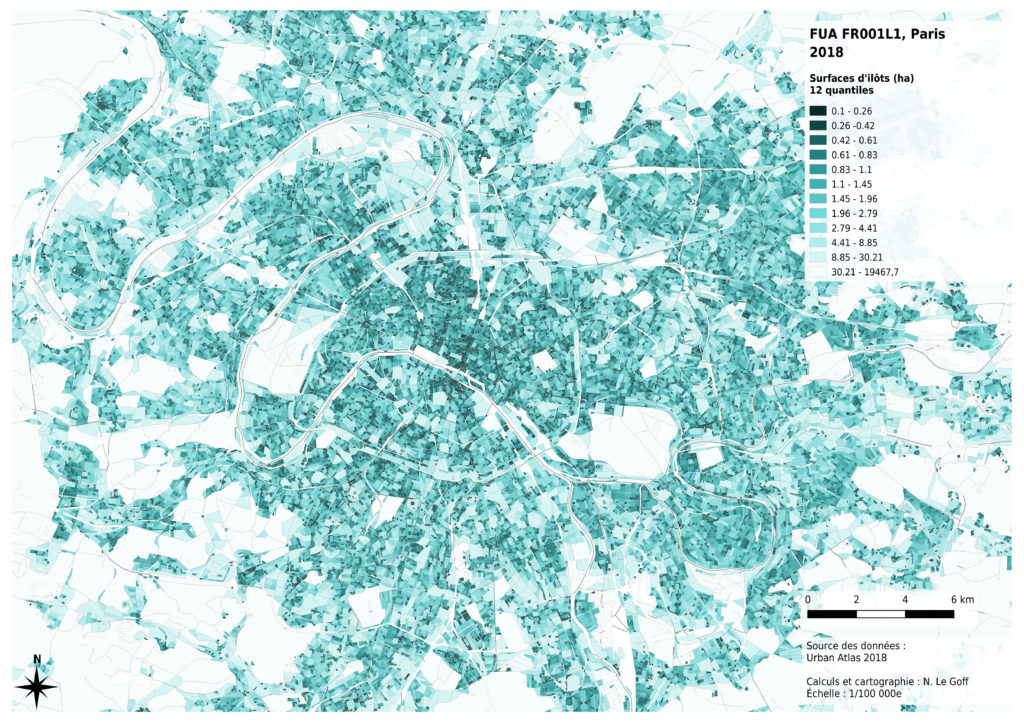
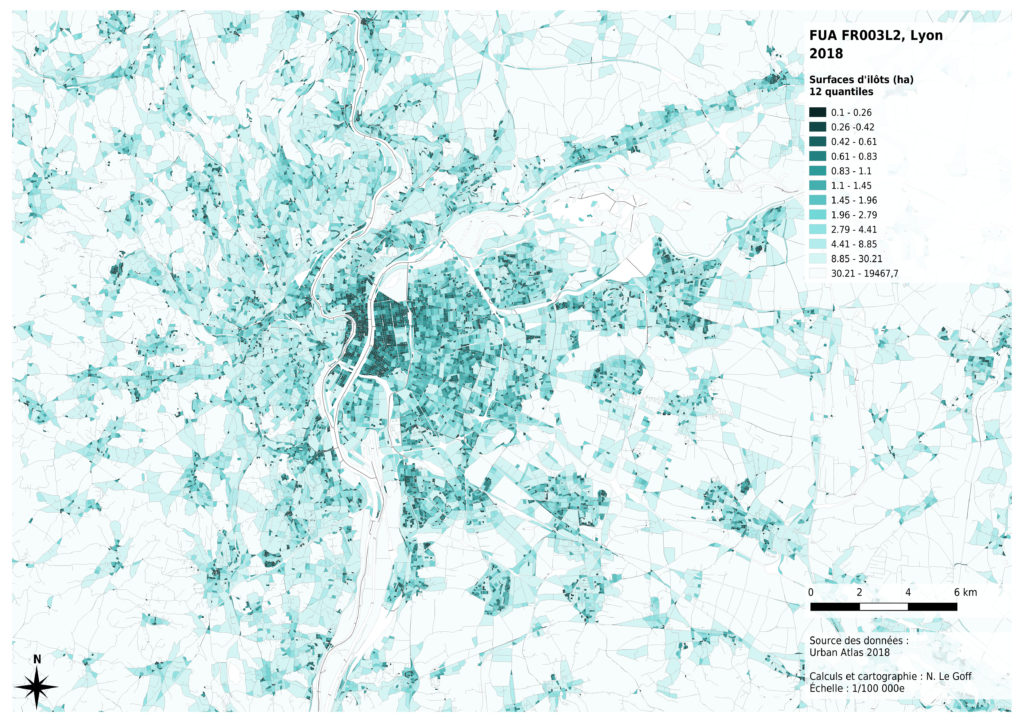
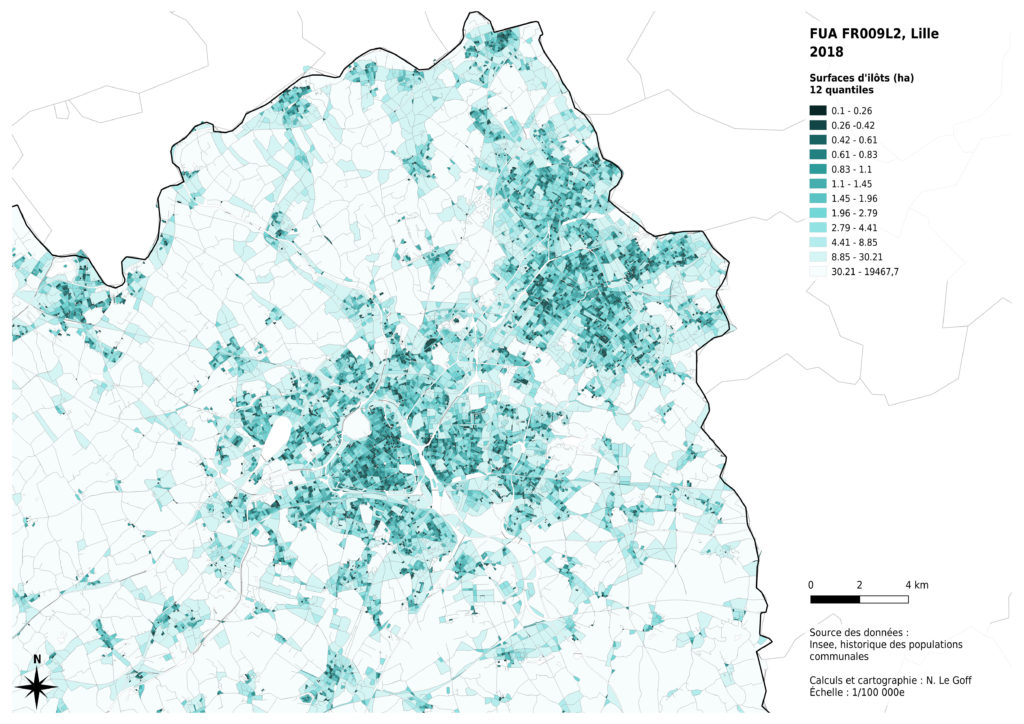
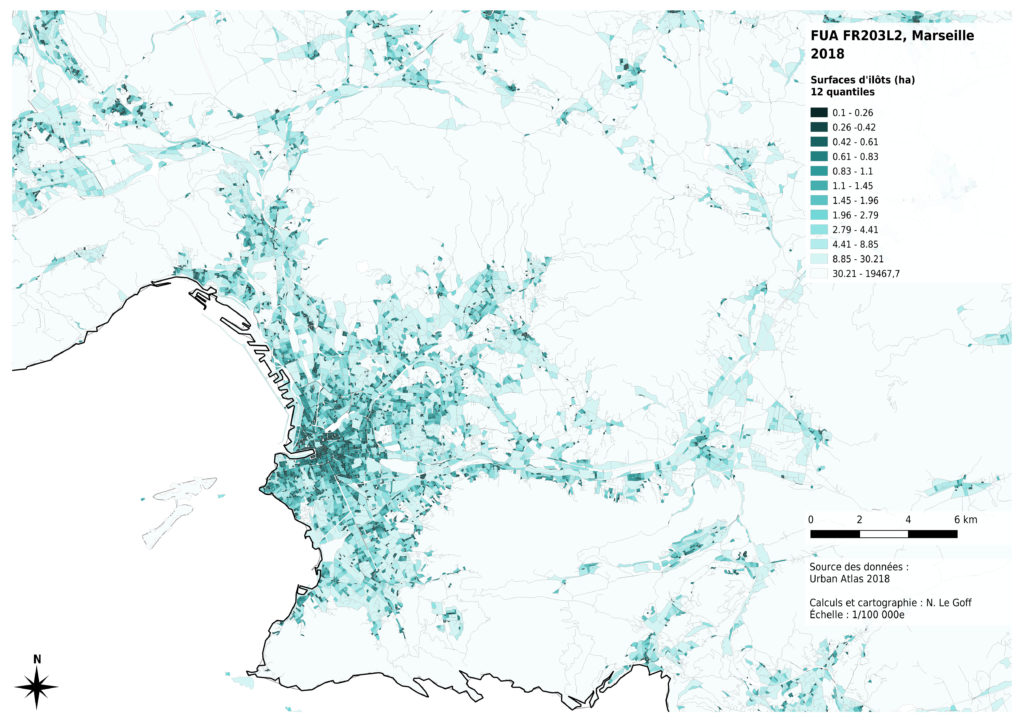
Nous avons commencé par tester la méthode des quantiles : 12 classes, comportant le même nombre d’îlots ont été créées.
Ce mode de représentation diminue les contrastes entre les plus grands îlots, qui sont en nombre moins importants, et augmente les contrastes entre les plus petites tailles d’îlots, qui constituent principalement les milieux urbanisés. Il est donc plutôt adapté à une analyse fine de l’hétérogénéité des surfaces d’îlots dans un tissu urbanisé, mais rend mal compte de la distribution des valeurs sur l’ensemble de la zone considérée.
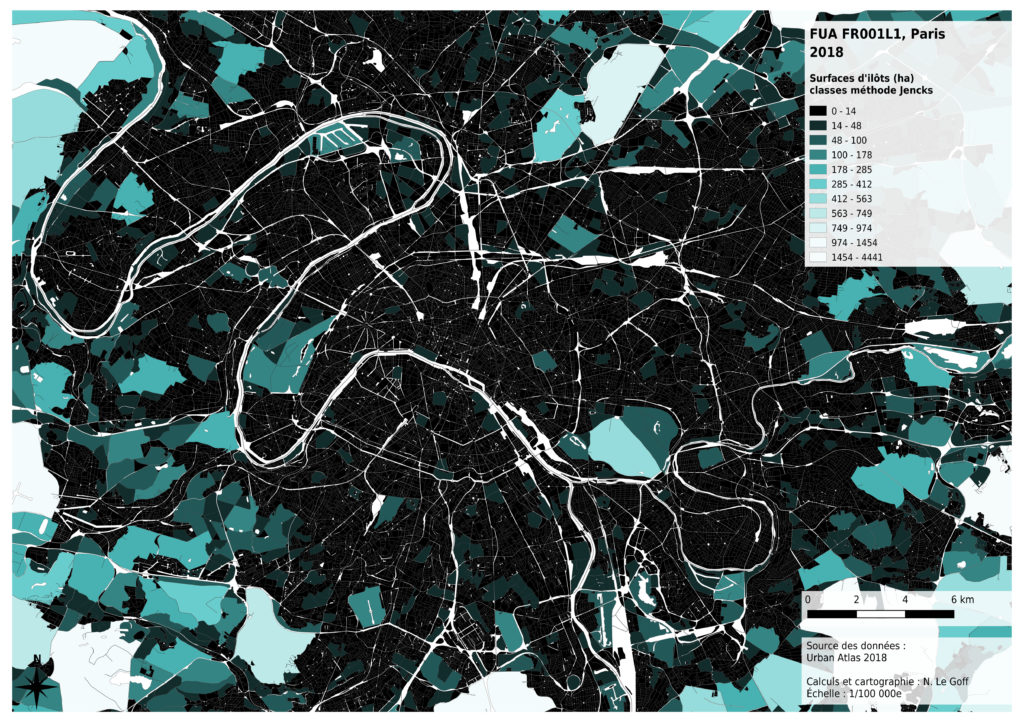
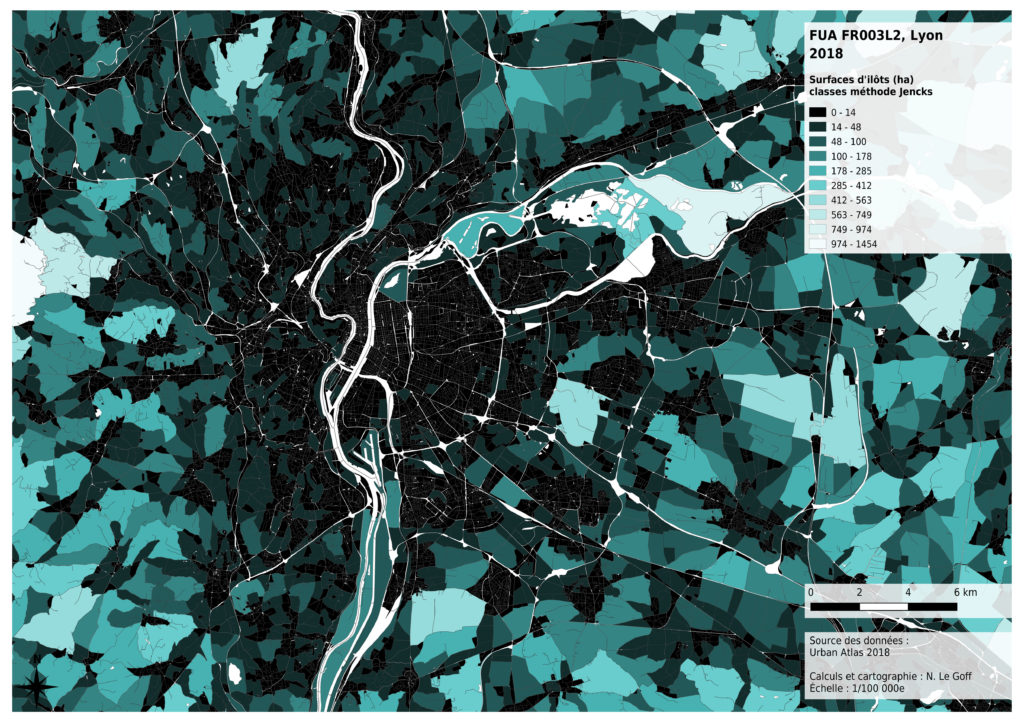
La méthode de Jencks est proposée par de nombreux logiciels de Sig et repose sur un calcul mathématique. Elle vise à regrouper par dans une même classe les valeurs dont la variance est minimale, tout en assurant une variance maximale entre les classes.
Cette méthode met en évidence les différences de surfaces des plus grands îlots dans les zones rurales ou naturelles, mais elle écrase les différences entre petits îlots, plus courants dans les zones urbanisées.
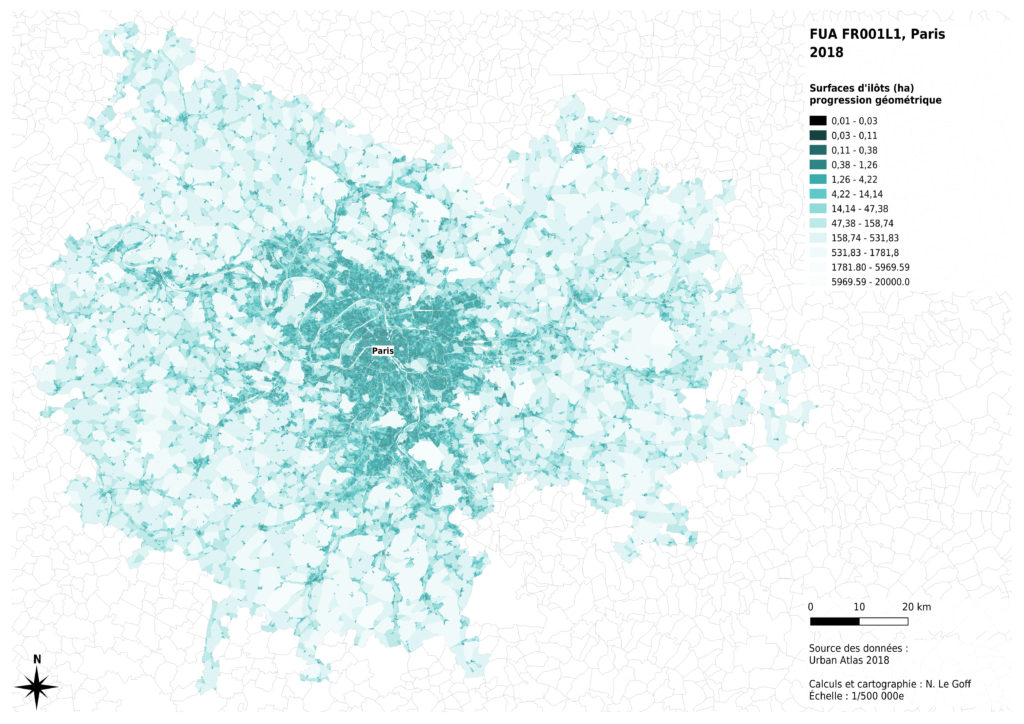
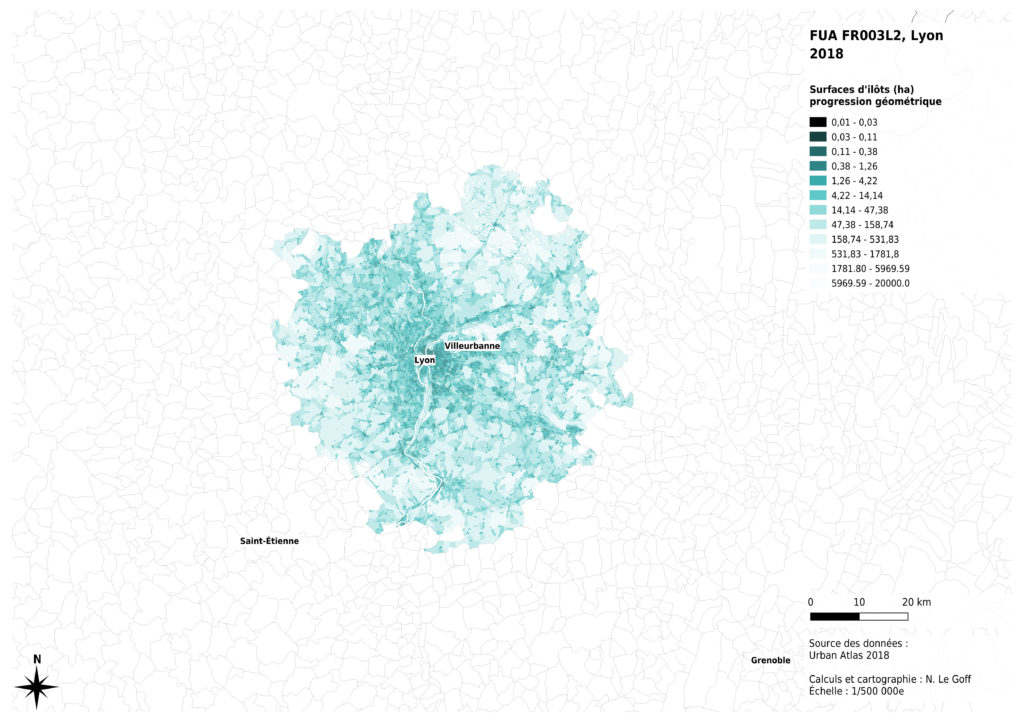
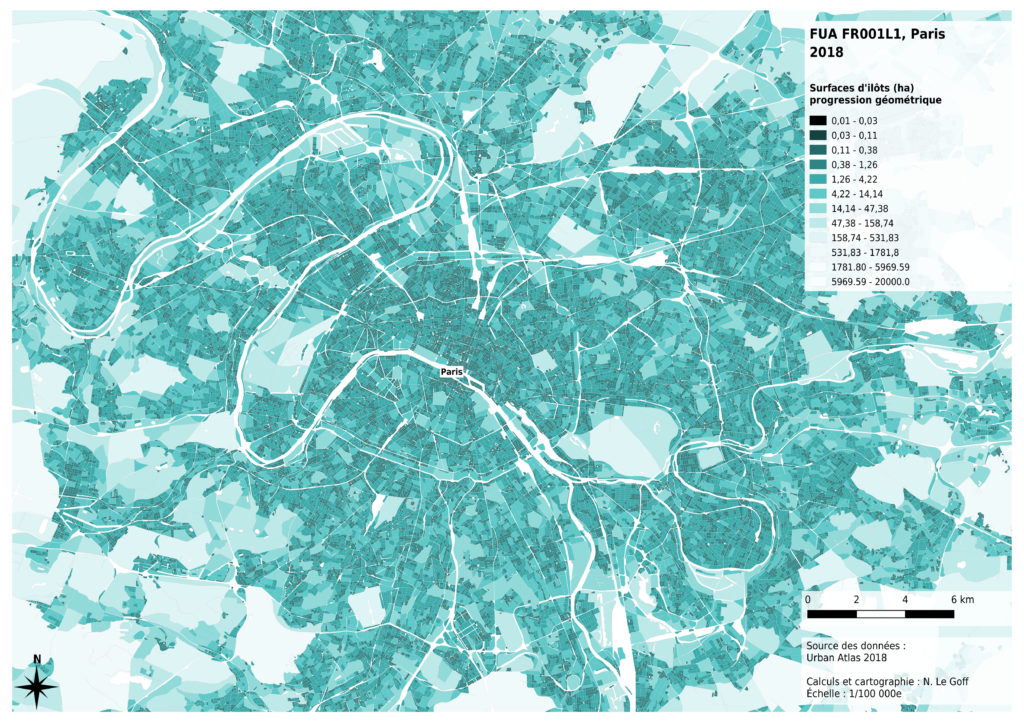
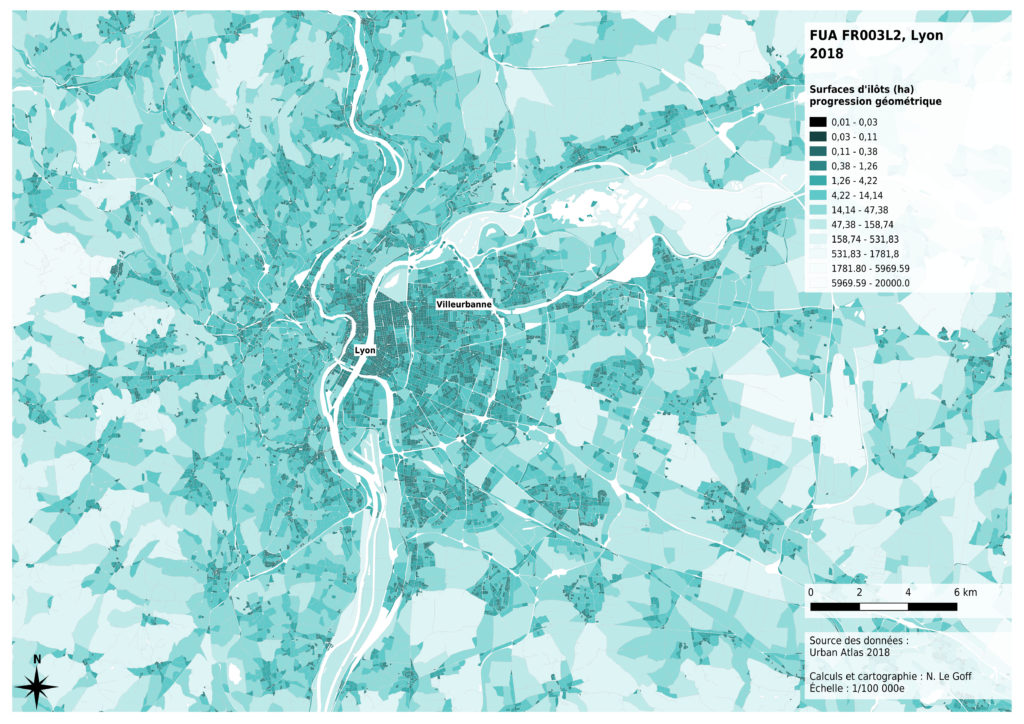
Comme la dispersion des valeurs est globalement exponentielle, c’est finalement la méthode de création de classes par progression géométrique qui nous a parue la plus pertinente, pour conserver un équilibre entre d’une part, l’analyse à l’échelle de l’agglomération et d’autre part, l’analyse plus fine des tissus urbains.
La limite de ce mode de représentation tient ici au dégradé linéaire de valeurs utilisé : la cartographie est visuellement trop homogène. Ce phénomène s’explique de plusieurs manières : d’une part, la perception des contrastes de luminosité par l’œil humain n’est pas identique pour les valeurs claires et foncées. Ce point, important pour la cartographie, est souligné par Jean-Luc Arnaud, dans Analyse spatiale, cartographie et histoire urbaine. Mais l’auteur ne fournit que quelques exemples d’échelles de gris, sans expliciter la méthode pour les réaliser.
Le grand coloriste qu’était Josef Albers a d’ailleurs aussi noté le même problème. Il a consacré sa vie à la question de la perception de la couleur. Très rationaliste – comme d’ailleurs certains de ses collègues du Bauhaus dans un contexte allemand des années 1920 où la Nouvelle Objectivité était forte en Allemagne- il a fait le lien entre ses propres observations de peintre, et les phénomènes documentés par Chevreul, Weber et Fechner. Dans son ouvrage de référence, L’interaction des couleurs, il insiste sur la nécessité d’établir des échelles de couleur du plus clair au plus foncé (dans un système soustractif, celui de la peinture), basé sur sur des progressions géométriques et non arithmétiques.
En pratique, cette méthode est difficile à appliquer dans les logiciels de Sig basés sur des systèmes de couleurs additifs. Par ailleurs, la loi de Weber-Fechner sur laquelle il appuie son raisonnement a depuis été critiquée : elle serait trop imprécise. La loi de Stevens est aujourd’hui plus utilisée, à travers notamment sa fonction de puissance et a trouvé ses applications dans l’élaboration de la notion de gamma pour les images numériques. Suite à différents essais, aucune de ces lois ne nous ont paru permettre de créer des échelles de couleurs dont la perception serait graduelle, à l’œil. Nous avons donc choisi de nous en inspirer en créant notre propre échelle à partir d’un dégradé linéaire de valeurs et en nous fiant à notre propre perception des couleurs.
Comme le note par ailleurs Josef Albers, la surface sur laquelle on applique une couleur a aussi des effets sur la perception que l’on en a. Dans le cas qui nous intéresse, les petits îlots, très foncés, ont des surfaces bien inférieures aux grands îlots, très clairs.
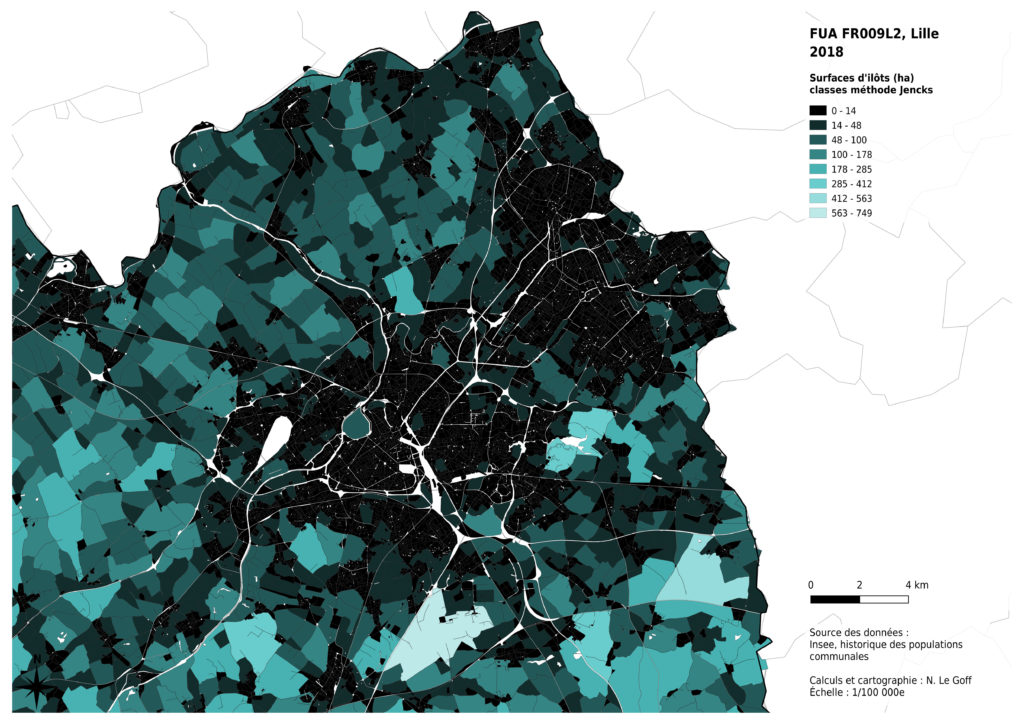
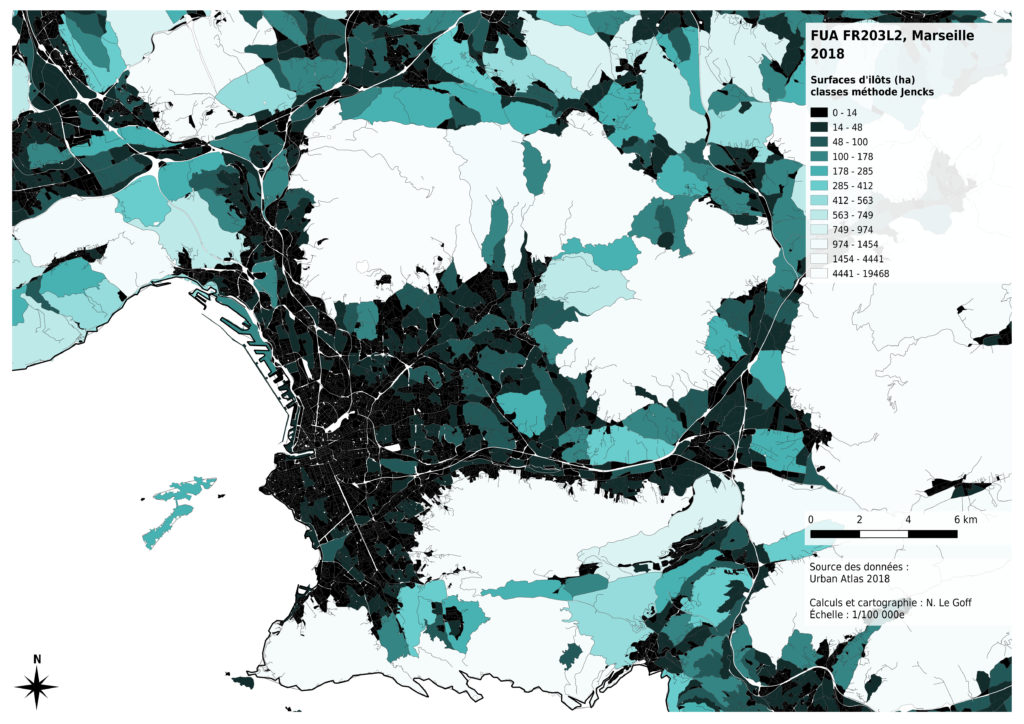
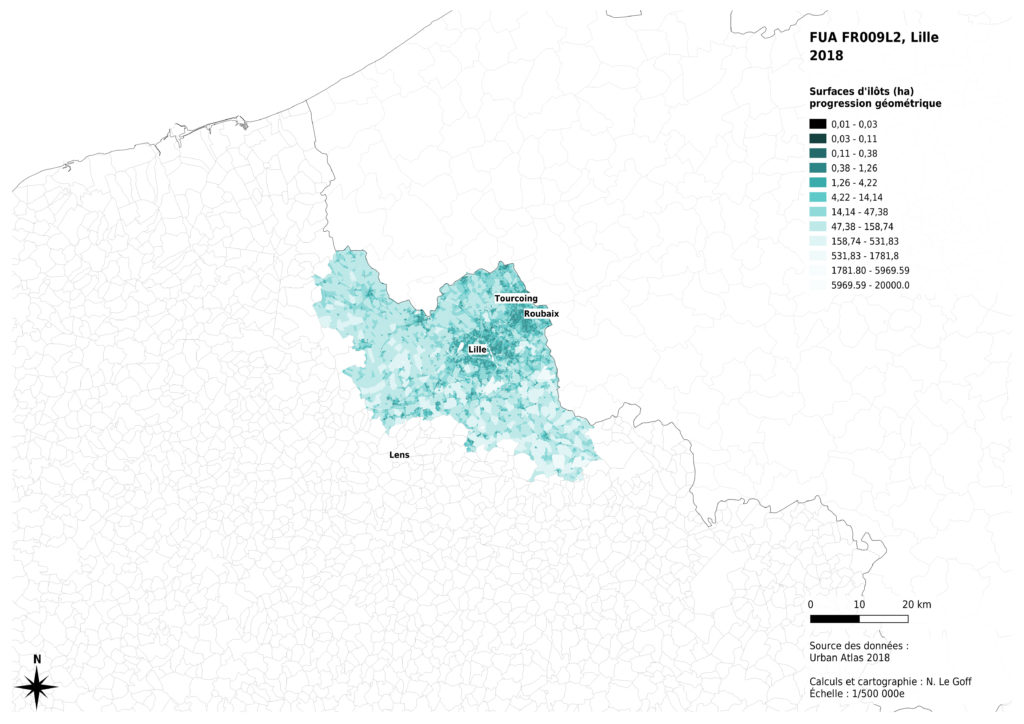
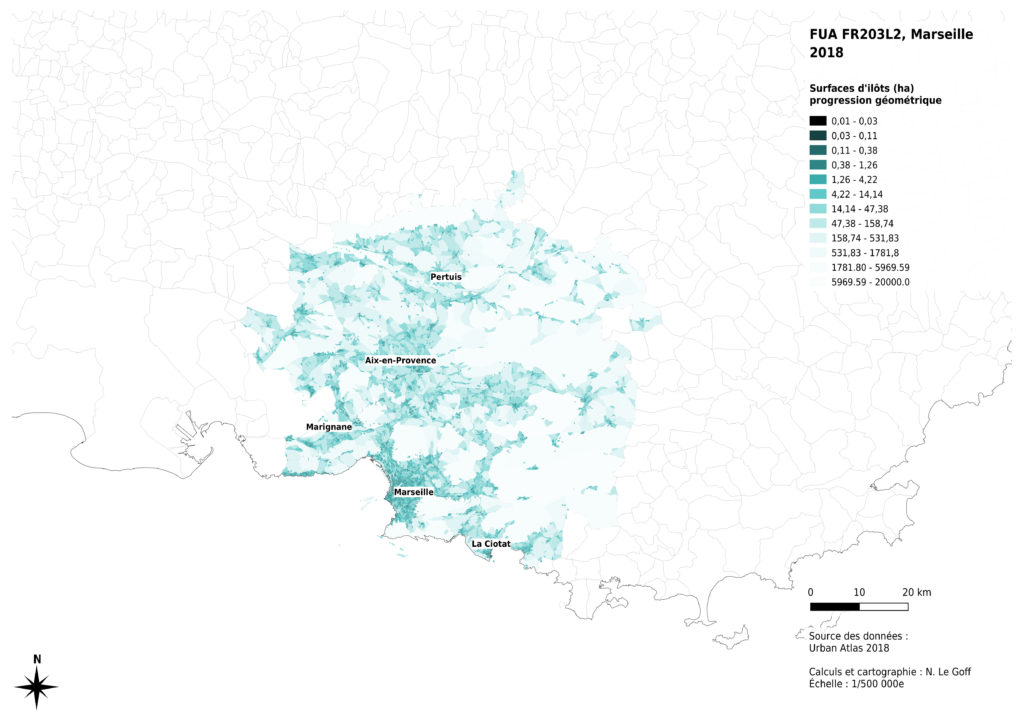
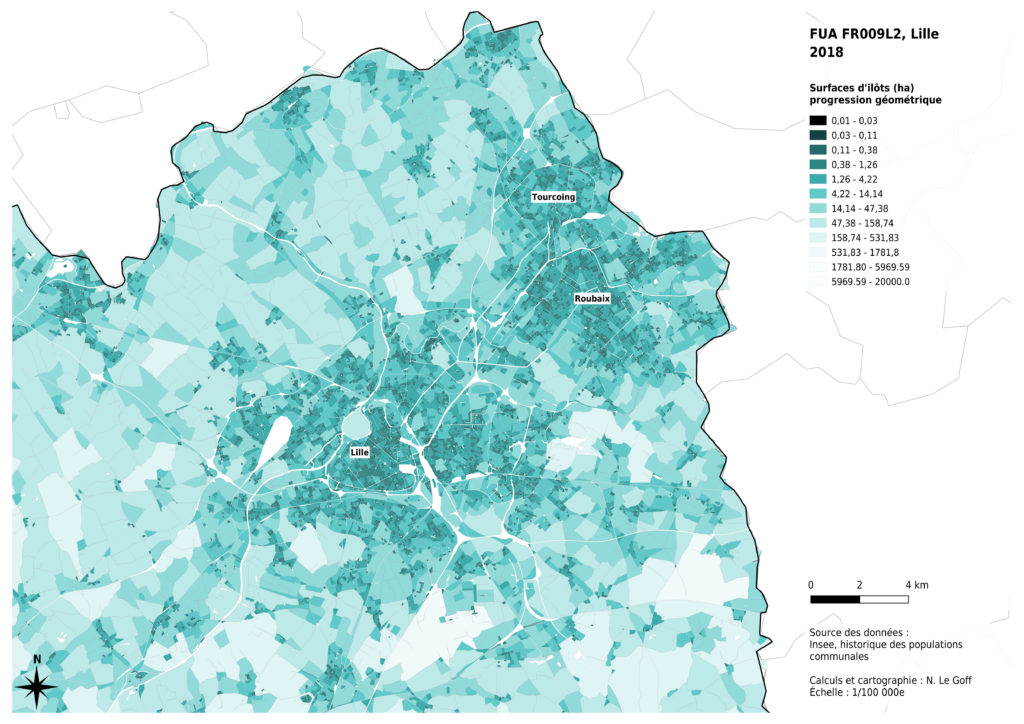
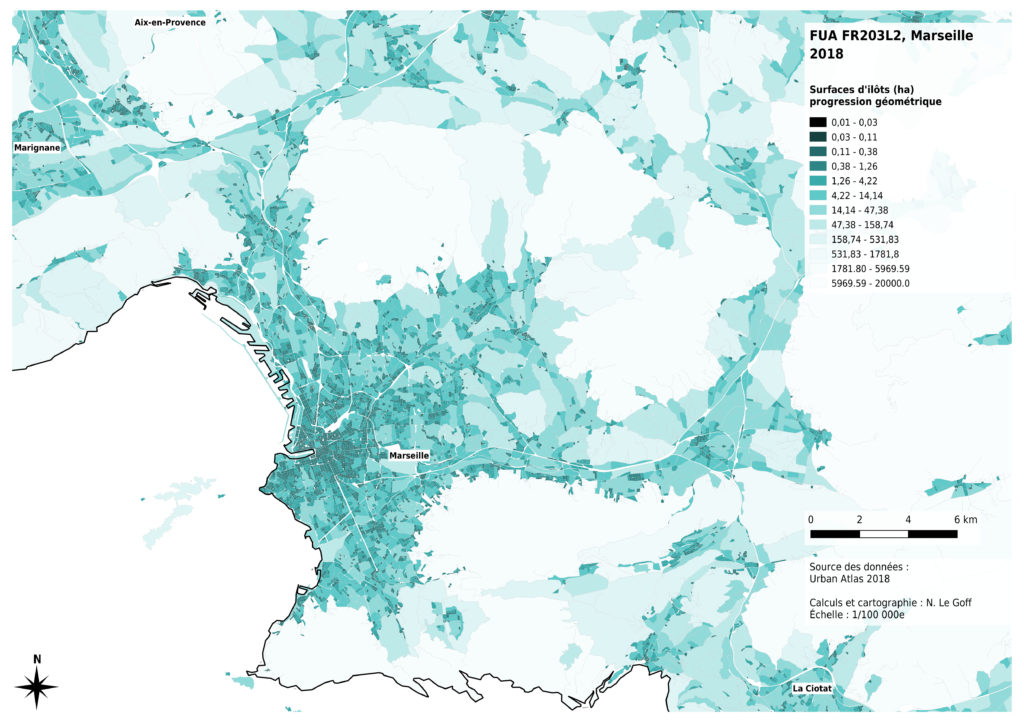
Enfin, l’analyse de la distribution des données montre que celle-ci n’est pas la même selon les métropoles concernées. La présence massive montagneux à proximité de Marseille a des effets sur les surfaces des îlots inclus dans la métropole : certains îlots sont très grands, par comparaison avec les autres cas. La région de Lille présente aussi des îlots ruraux globalement plus petits, probablement du fait de l’histoire de l’occupation du sol à des fins agricoles. Nous avons donc choisi de diminuer les contrastes entre les valeurs claires de notre dégradé de couleurs pour permettre une comparaison visuelle entre les 4 cas analysés.
Si l’on cherche la valeur médiane des surfaces d’îlots pour l’ensemble des 4 cas concernés, on obtient une valeur qui peut servir de référence pour une comparaison plus fine entre ces cas. Cette approche permet de mettre en évidence visuellement plusieurs éléments.